. . . is a piece that was composed over a period of a year & a half.  I composed them out of order;

the second one coming first.  These are indeed three

separate mechanisms; each of them having their own method of creation. 

Some Technical Information on the Second Movement (if you are interested)

This second movement, was composed

using a mathematical system of the arrangement of the numerical sequence :     1 2 3 4 5 6 7

        This sequence sounds pretty basic, but that is the beauty of it.  I then take a modular formula

(found in "modular arithmetic") to obtain the numerical series that I want. 

In modular arithmetic, you are dealing with a circular formation of numbers. 

& what you are thinking right now IS : "What the HELL is this guy talking about?  Right?" 

Well, everyday, human beings whom live with time, deal with modular arithmetic, & does not even

know they are doing it.  

PROOF:  Someone is asked to meet at an appointment in 3 hrs. & the time is now 10am. 

Now in normal math 10 + 3 is 13, BUT in modular arithmetic,

the answer is 1(if of course you are NOT in the military).  SEE!!!

So the formula I used is as follows :

                x-1-1(mod7)     x-2-1(mod7)    x-3-1(mod7)    x-4-1(mod7)     x-5-1(mod7)    x-6-1(mod7)    x-7-1(mod7)  

     **but in order to obtain the next "x" term, you must add "x" to itself.  Sounds complicated, but it's not.**

I'll give you a start on the numeric sequence that this formula gives with the base sequence of 1 - 7.

            First start with x=1

            x-1-1(mod7) = 1-1-1    which equals 6    Then to obtain the next "x", add 6 to itself      6+6(mod7)=5

            x-2-1(mod7) = 5-2-1    which equals 2    Then again add "x" to itself    2+2(mod7)=4

            x-3-1(mod7) = 4-3-1    which equals 7

            . . . . . . . etc . . . . . . . until it repeats after 21 times through.  The first three are exemplified here.

        Then when I finished with this, I broke the numbers into subgroups.   Example is the first 6 : being turned into

1 + 4 + 1.  Then assigned an eighth note to the number 1.   So the first 6 in musical terms would be

eighth + 4eighths + eighth.

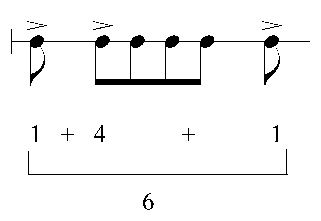
So there's the introduction of the process used for the Marimba part's rhythmic sequence.

If anyone is crazy enough to hear the rest or get any clarifications,

LET ME KNOW - "Contact ME"!!!

                                                             Duration of the Mechanisms:

                                                                                                                                    I.      6.02'

                                                                                                                                   II.     1.05'

                                                                                                                                  III.     3.54'